When I starting to think about doing a blog on the occurrence of Fibonacci sequences in Nature, the phrase Fibonacci gnocchi floated into my brain. I’m not sure why! The words just sounded nice; I had no idea that such a think might actually exit! Well Leonardo Bonacci, commonly known as Fibonacci, was Italian, so it is possible that he liked gnocchi! See final paragraph for details on Fibonacci gnocchi!

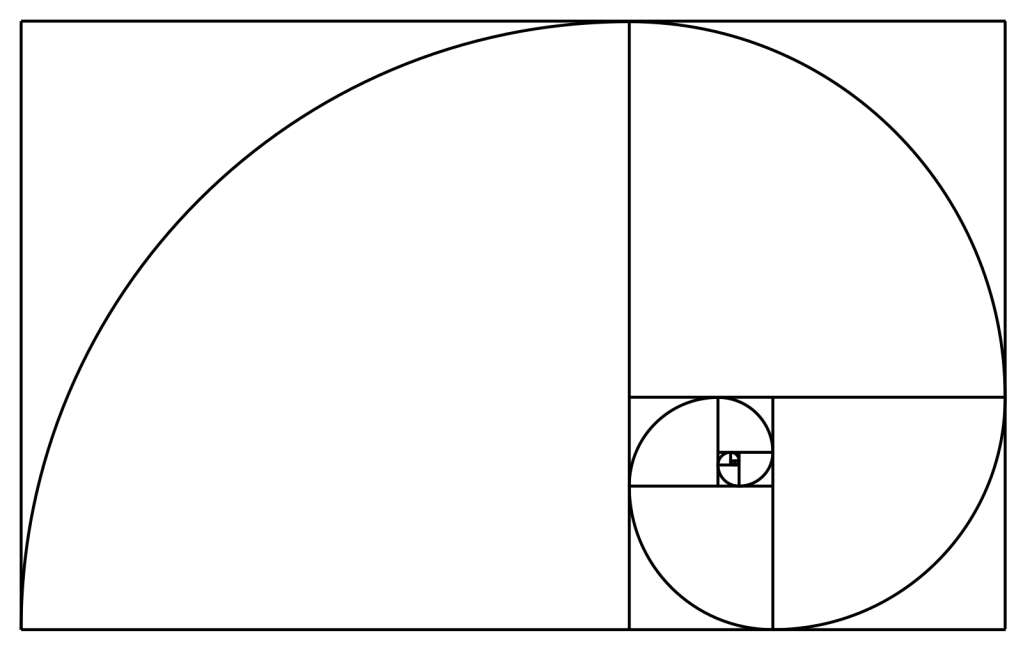
First of all, let’s establish what it is. The Fibonacci Sequence is a mathematical pattern where each number is the sum of the two preceding ones: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 etc. This number pattern, in which the basic units can be grouped into clockwise and counter-clockwise spirals, is found in many plants, including cacti, pine cones, sunflowers, daisies and so on. Even rose buds are a form of Fibonacci spirals, as are strawberries, blackberries and raspberries.

The other extraordinary property of the Fibonacci sequence is its relationship to the golden ratio, which is approximately 1.618 and usually represented by the Greek letter phi (φ). As the Fibonacci numbers increase, the ratio between consecutive numbers start to approach this value: e.g. 21 divided by 13 equals 1.615, and 34 divided by 21 equals 1.619, close to the golden ratio.

One very attractive example of a Fibonacci spiral occurs in Woolly thistles (Cirsium eriophorum), which I mentioned in a previous blog. The large flower head, up to 70mm across, is almost spherical apart from the slightly flattened top where the Fibonacci spiral of spines originate (see below).

Anyway, my aim here is simply to show off some images of Fibonacci spirals from my photo collection. Not to get get caught up in the maths (math if you are American!), which was never my favourite subject! Readers can follow the links to the equations if they like.

Protea flower buds also form beautiful Fibonacci spirals (below).

Teasel flower and seed heads also exhibit a Fibonacci spiral. The bracts are arranged in opposing spiral patterns, with the number of spirals in each direction typically corresponding to consecutive numbers in the Fibonacci sequence (below). 

Anyway, returning to the idea of Fibonacci gnocchi, at least two people have created images of Fibonacci spirals made of gnocchi (pasta-like potato dumplings): see here and here. Gnocchi is one of my favourite dishes, whether it occurs in spirals or not! Here (below) is a picture of a young lady making gnocchi (I think!) in a restaurant in Florence, I snapped as I walked past one evening.

Fibonacci spirals form in flowers as they grow, with the new buds or seeds emerging from a central point, with each new bud pushing the previously formed ones radially outward. This pattern allows plants to pack the maximum number of seeds or petals into a given space, and spiral packing also provides structural stability to the flower head or plant.